Pada artikel sebelumnya yang berjudul Konsep Ketidakpastian Pengukuran di Laboratorium Berdasarkan ISO, Saya menjelaskan tentang definisi dari ketidakpastian dan sumber-sumber ketidakpastian pengukuran. Artikel ini melanjutkan pembahasan tersebut yaitu mengenai perhitungan ketidakpastian pengujian.

Pada umumnya, ada 2 pendekatan yang biasa kita pakai untuk perhitungan ketidakpastian yaitu:   

1. Pendekatan Pemodelan (Bottom-up approach)

Pada evaluasi ketidakpastian dengan menggunakan pendekatan ini, memperhitungkan semua sumber ketidakpastian secara individual. Sumber ketidakpastian tersebut antara lain dari massa,  volume, konsentrasi standar, dan sebagainya. Setelah itu, menggunakan pendekatan model matematik untuk  menggabungkannya. Biasanya, metode ini menggunakan diagram tulang ikan, sehingga metode ini lebih terkenal dengan nama metode fishbone.

Tahap pertama, kita harus mengidentifikasi setiap tahap analisis yang terpisah, kemudian menetapkan seluruh komponen ketidakpastian yang sesuai. Setelah itu, menggabungkan seluruh komponen tersebut dengan menggunakan model matematis untuk memberikan nilai ketidakpastian keseluruhan. Terakhir, mengalikan dengan faktor cakupan untuk mendapatkan ketidakpastian yang diperluas.

2. Pendekatan Empiris (Top-down approach)

Pendekatan metode perhitungan ketidakpastian pengujian ini menggunakan replikasi dari seluruh prosedur pengukuran untuk memberikan perkiraan langsung dari ketidakpastian untuk hasil akhir pengukuran. Pada metode ini, kita bisa menggunakan data presisi dan bias dari pengujian CRM ataupun uji profisiensi sebagai data evaluasi ketidakpastian pengukuran.

Pada dasarnya, metode ini mengevaluasi komponen-komponen ketidakpastian menggunakan real data dari suatu seri pengukuran/pengujian yang kita kerjakan di laboratorium. Penerapan metode ini antara lain pada pengujian kuantitatif mikrobiologi dan kimia yang mengandalkan perkiraan reproduktifitas dan bias. Lebih lanjut, pembahasan metode Top down ini ada pada artikel selanjutnya.

Metode Fishbone (Bottom-up approach)

Sebelum berlanjut untuk membahas tentang tahapan dalam perhitungan ketidakpastian pengujian metode ini, berikut kelebihan dan kekurangan metode Bottom-up (metode fishbone) :

Kelebihan

• Mengidentifikasi semua sumber kesalahan sehingga memberikan perkiraan yang lebih baik.
• Bisa kita aplikasikan untuk semua metode analisis kimia dan mikrobiologi kuantitatif.

Kekurangan

• Ada beberapa sumber kesalahan dalam pengukuran yang analis sulit mengevaluasi ketidakpastiannya.
• Perhitungan membutuhkan waktu yang lebih lama.
• Langkah perhitungan lebih panjang untuk metode analisis yang mempunyai langkah kerja yang rumit dan menggunakan peralatan yang banyak.

Tahapan dalam melakukan perhitungan ketidakpastian pengujian

1. Menentukan spesifikasi kuantitas pengukuran

Pada tahap ini, kita harus menentukan spesifikasi kuantitas pengukuran. Evaluasi ketidakpastian metode fishbone mendasarkan pada formula atau rumus perhitungan dan  komponen-komponen lain yang tidak ada dalam rumus namun juga mempunyai pengaruh terhadap ketidakpastian.

2. Identifikasi sumber ketidakpastian.

a. Membuat daftar dari semua sumber ketidakpastian.

Dalam memperkirakan daftar sumber ketidakpastian yang kita perlukan, lebih mudah untuk memulai dengan menggunakan formula atau rumus untuk menghitung besaran ukur. Semua parameter dalam ekspresi ini memiliki ketidakpastian yang terkait dengan nilainya sehingga ini merupakan potensi sumber ketidakpastian. Selain itu, mungkin ada parameter lain yang tidak muncul secara eksplisit dalam ekspresi yang kita gunakan untuk menghitung nilai besaran ukur, namun tetap mempengaruhi hasil pengukuran. Sebagai contoh ketidakpastian dari suhu pemanasan, kesalahan acak dan sistematik yang juga merupakan sumber ketidakpastian potensial. Semua sumber tersebut harus dimasukkan.

b. Membuat diagram fishbone.

Diagram sebab dan akibat adalah salah satu tool untuk menginventarisir daftar sumber ketidakpastian dan memberikan gambaran jelas bagaimana mereka berhubungan satu sama lain dan menunjukkan pengaruhnya terhadap ketidakpastian hasil. Metode ini juga membantu menghindari sumber ketidakpastian yang terhitung secara gandav (double counting).

3. Kuantifikasi komponen ketidakpastian

Setelah mengidentifikasi sumber ketidakpastian, langkah selanjutnya adalah mengukur ketidakpastian yang muncul dari sumber tersebut dengan mengevaluasi ketidakpastian yang timbul dari masing-masing sumber dan menggabungkannya. Ada juga cara lain yaitu dengan menentukan secara langsung kontribusi gabungan terhadap ketidakpastian hasil dari beberapa atau semua sumber ini menggunakan data kinerja metode.

Sebagian besar informasi yang kita perlukan untuk mengevaluasi ketidakpastian terkadang sudah tersedia dari proses pemeriksaan kinerja metode seperti hasil studi validasi, dari data QA / QC dan dari pekerjaan eksperimental lain. Akan tetapi, ada data yang mungkin tidak tersedia dari literatur ataupun dari hasil pemeriksaan kinerja metode. Dalam hal ini, kita perlu melakukan ekseprimen lebih lanjut. Berikut penjabaran tipe estimasi ketidakpastian.

Tipe estimasi ketidakpastian  Evaluasi tipe A

• Berdasarkan pekerjaan percobaan dan  menghitung rangkaian berulang
• Evaluasi komponen ketidakpastian  menggunakan cara statistik

Tipe estimasi ketidakpastian  Evaluasi tipe B

Berdasarkan informasi yang terpercaya menggunakan semua informasi  relevan yang tersedia, meliputi :

• nilai acuan dari standar/pustaka, volume labu  volumetrik, pipet
• variasi suhu ruang pengujian
• Data yang ada dalam sertifikat atau  laporan lainnya
• Spesifikasi pabrik

Tingkat kepercayaan 95%

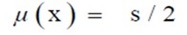
Tingkat kepercayaan 99%

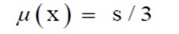
Apabila informasi datanya tidak ada keterangan apapun maka bisa mengasumsikan sebagai distribusi  rektangular

Untuk distribusi triangular atau distribusi sempit

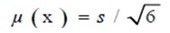
berikut bagan perbedaan antara tipe A dan tipe B

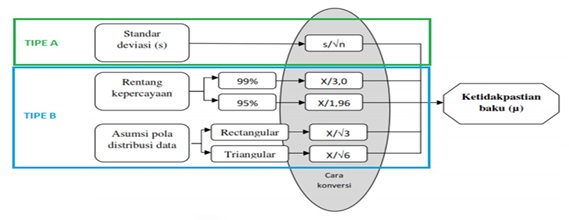
Pada dasarnya, tidak semua komponen ketidakpastian memberikan kontribusi yang signifikan terhadap nilai ketidakpastian gabungan. Dalam prakteknya, ada beberapa sumber ketidakpastian yang memiliki nilai yang tidak memberikan kontribusi nyata dalam perubahan nilai ketidakpastian. Umumnya, komponen yang mengandung nilai kurang dari sepertiga nilai ketidakpastian terbesar akan tidak perlu masuk dalam perhitungan. Namun begitu, Estimasi awal tentang kontribusi setiap komponen atau kombinasi komponen terhadap ketidakpastian harus dibuat untuk memastikan nilainya terlebih dahulu.

4. Perhitungan ketidakpastian gabungan

Sebelum menghitung ketidakpastian gabungan, semua kontribusi ketidakpastian harus menjadi bentuk ketidakpastian bakunya. Setelah estimasi individu atau kelompok komponen ketidakpastian menjadi ketidakpastian baku, tahap selanjutnya adalah menghitung ketidakpastian baku gabungan menggunakan aturan berikut.

a. Aturan penjumlahan atau pengurangan.  Model : Y = a + b + c

Ketidakpastian gabungan :

µc (Y) =

b. Aturan perkalian atau pembagian.  Model Y = a. b. c atau a. b/c

Ketidakpastian gabungan :

µc (Y) = 

c. Aturan yang melibatkan pangkat.  Model : Y = a^n

Ketidakpastian gabungan

µc (Y) = 

5. Ketidakpastian diperluas

Ketidakpastian baku gabungan yang diperoleh, kita kalikan dengan faktor cakupan untuk mendapatkan nilai tersebut. untuk lebih jelasnya, berikut cara perhitungannya :

U = k x µc (Y)

Untuk ketidakpastian diperluas pada tingkat kepercayaan 95% digunakan faktor cakupan

(k) = 1,96 atau 2. Umumnya penggunakaan  k adalah sama dengan 2. Namun, nilai k ini mungkin tidak sesuai ketika ketidakpastian gabungan menggunakan pengamatan statistik dengan derajat kebebasan yang relatif sedikit (kurang dari sekitar enam). Pilihan k kemudian tergantung pada jumlah derajat kebebasan efektif.

6. Pelaporan hasil pengujian

Pembuatan laporan hasil uji dan ketidakpastian menggunakan formula

( Y ± U ) (satuan)

dengan menambahkan pernyataan tingkat kepercayaan dan faktor cakupan.

Enam tahapan perhitungan ketidakpastian pengujian secara bottom-up approach ini merupakan metode yang umum. Banyak praktisi yang menggunakan cara ini. Tapi apakah cara ini merupakan cara terbaik? Pada kesempatan yang akan datang akan Saya bagikan cara perhitungan ketidakpastian pengujian dengan teknik top-down.