Dalam dunia pengukuran dan analisis data, termasuk laboratorium, ketidakpastian merupakan hal yang tak terhindarkan. Ketidakpastian pengukuran merujuk pada ketidakpastian atau kesalahan yang terkait dengan nilai yang dihasilkan dari suatu pengukuran. Oleh karena itu kita sebagai praktisi laboratorium perlu memahami tipe a dan tipe b dalam estimasi ketidakpastian dengan baik.

Baca juga: Konsep Ketidakpastian Pengukuran di Laboratorium Berdasarkan ISO

Dalam upaya untuk menggambarkan nilai ketidakpastian ini, konsep tipe A dan tipe B sering digunakan untuk mengklasifikasikan pendekatan yang berbeda dalam mengestimasi ketidakpastian pengukuran.

Mari kita lihat lebih dekat masing-masing tipe ini dalam konteks estimasi ketidakpastian pengukuran.

Ketidakpastian Baku Tipe A

Tipe A dalam estimasi ketidakpastian pengukuran mengacu pada pendekatan yang berdasarkan pada analisis statistik dari hasil pengukuran yang ada. Metode ini mencakup penggunaan statistik deskriptif, seperti perhitungan rata-rata dan standar deviasi, untuk mengestimasi ketidakpastian.

Dalam tipe A, pengukuran yang dilakukan secara berulang pada sampel yang sama digunakan untuk memperoleh estimasi statistik yang dapat kita gunakan untuk menggambarkan ketidakpastian. Pendekatan ini terutama kita gunakan ketika data pengukuran yang cukup tersedia.

Cara Menghitung Ketidakpastian Tipe A

Dalam menghitung ketidakpastian tipe A, kita perlu melakukan serangkaian pengulangan percobaan yang pada akhirnya bisa kita tarik nilai deviasi data tersebut. Nilai standar deviasi ini yang akan kita gunakan untuk menghitung nilai standar error. Pada akhirnya SE atau standar error adalah sama dengan ketidakpastian baku (tipe A).

Rumus perhitungan nilai standar error atau ketidakpastian baku tipe A adalah sebagai berikut:

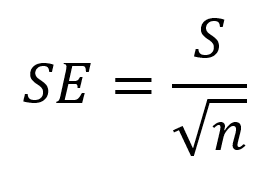
Dengan S adalah standar deviasi dan n adalah jumlah ulangan pengukuran. Standar deviasi sendiri merupakan suatu ukuran seberapa dekat hasil-hasil individual terhadap nilai rata-ratanya. Secara Matematika, standar deviasi bisa kita dapatkan dengan menggunakan rumus berikut ini:

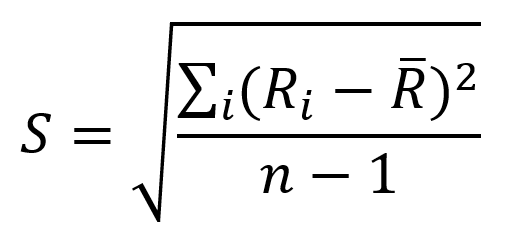
Tentu saja akan lebih mudah jika kita menghitung standar deviasi menggunakan kalkulator atau excel.

Ketidakpastian Baku Tipe B

Tipe B dalam estimasi ketidakpastian pengukuran mengacu pada pendekatan yang berdasarkan pada penilaian subjektif atau pemodelan. Metode ini mencakup penggunaan pengetahuan atau informasi yang tersedia secara kualitatif untuk memperoleh estimasi ketidakpastian.

Dalam tipe B, berbagai faktor seperti pengalaman ahli, informasi dari literatur, atau analisis permodelan akan kita gunakan untuk mengestimasi ketidakpastian. Pendekatan ini kita terapkan ketika data pengukuran yang tepat atau cukup tidak tersedia, atau ketika situasi pengukuran tidak dapat kita replikasi secara langsung.

Bagaimana Cara menghitung Ketidakpastian Baku Tipe Ini?

Jika ketidakpastian baku tipe A menggunakan standar error, lalu bagaimana dengan tipe B? Dalam menghitung ketidakpastian, baik tipe A maupun tipe B ini kita perlu memahami konsep distribusi probabilitas. Karena semua sangat terkait dengan distribusi probabilitas.

Terdapat beberapa bentuk distribusi probabilitas yang perlu kita pahami sebelum lebih jauh mempelajari estimasi ketidakpastian. Beberapa distribusi probabilitas itu adalah normal, kotak, dan segitiga. Secara total tidak hanya tiga model distribusi ini, tapi setidaknya ketiga ini lah yang harus kita pahami dalam konteks estimasi ketidakpastian, dan akan sering kita temui kondisinya saat perhitungan nanti.

Ketidakpastian Baku Pada Kondisi Distribusi Normal

Suatu data akan terdistribusi secara normal apabila rata-rata nilai variabel sama dengan median begitu pula dengan modus nilai data tersebut. Distribusi ini juga dijuluki kurva lonceng (bell curve) karena grafik fungsi kepekatan probabilitasnya mirip dengan bentuk lonceng.

Model distribusi probabilitas normal ini sangat umum kita jumpai. Distribusi normal memodelkan fenomena kuantitatif pada ilmu alam dan ilmu sosial, dan lain sebagainya. contoh yang bisa kita asumsikan terjadi secara normal yaitu seperti nilai kelulusan sekelompok siswa sekolah, tinggi badan anak usia remaja yang terdistribusi antara 150 cm hingga 165 cm misalnya, dan lainnya.

Pada saat kita mengambil suatu nilai ketidakpastian dari suatu sumber informasi, kita pun perlu mengetahui berapa rentang kepercayaan yang nilai tersebut dapatkan. Walaupun tidak mutlak, umumnya para praktisi menggunakan rentang kepercayaan 95% dan 99% dalam model distribusi probabilitas normal.

Rentang kepercayaan ini akan terkait dengan berapa faktor pembagi yang akan kita gunakan dalam menentukan ketidakpastian baku. Pada saat rentang kepercayaan 95% maka faktor pembaginya adalah 1,96 atau 2 jika kita bulatkan. Pada saat rentang kepercayaan 99% maka faktor pembaginya adalah 3.

Sebagai contoh, kita mengambil informasi ketidakpastian dari sertifikat kalibrasi. Biasanya sertifikat tersebut juga mencamtumkan berapa rentang kepercayaan yang ia gunakan. Nilai yang disebutkan oleh labu takar 100 mL misalnya adalah: 100+/-1 mL pada rentang kepercayaan 95%. Jika ia menyebutkan 95% sebagai rentang kepercayaan yang ia gunakan, maka kita bisa gunakan 1,96 sebagai pembagi.

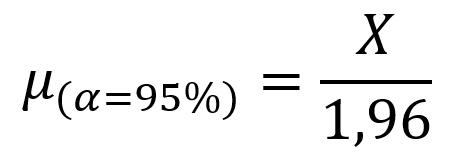
Ketidakpastian Baku Pada Kondisi Distribusi Probabilitas Kotak

Distribusi ini didasarkan pada asumsi bahwa ada batas berhingga dari tersebarnya nilai-nilai, tetapi tidak cukup informasi yang menunjukan nilai-nilai mana saja yang lebih mungkin, sehingga diambil kebolehjadian yang sama untuk setiap nilai. Rentang sebaran biasanya dapat dipandang simetris di sekitar nilai rata-rata. Distribusi probabilitas kotak tergambarkan sebagai berikut.

Jika model distribusi normal menggambarkan kondisi yang terjadi secara alami, maka pada model distribusi kotak adalah sebaliknya. Beberapa keadaan yang biasanya kita paksakan seperti pada proses produksi industri, akan menghasilkan produk-produk dengan sebaran dengan frekuensi sama sehingga jika kita gambarkan dengan grafik akan membentuk pola kotak.

Pada keadaan normal pasti ada satu atau dua orang yang sangat tinggi atau sangat pendek yang masuk ke dalam populasi, namun tidak jika kita membuat suatu produk. Misalnya saja produk pensil. Pensil hasil produksi yang panjangnya melebihi syarat akan kita buang. Karena ada intervensi tersebut maka distribusi kotak bisa terjadi.

Pada kondisi ini, maka faktor pembagi yang kita gunakan untuk menentukan nilai ketidakpastian baku adalah akar tiga.

Ketidakpastian Baku Pada Kondisi Distribusi Probabilitas Segitiga

Distribusi ini didasarkan pada adanya keyakinan bahwa nilai-nilai yg lebih dekat ke nilai rata-rata memiliki kebolehjadian yang lebih tinggi, dan nilai-nilai yang lebih dekat dengan batas rentang kebolehjadiannya berkurang menuju nol. Secara visual sebagai berikut:

Pada kondisi ini, maka faktor pembagi yang kita gunakan untuk menentukan nilai ketidakpastian baku adalah akar enam.

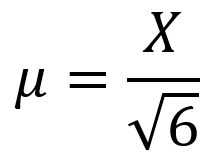
Kesimpulan

Penting untuk memahami bahwa kedua tipe ini (A dan B) saling melengkapi dan dapat kita gunakan secara bersama-sama dalam estimasi ketidakpastian pengukuran. Tipe A dan tipe B sering kali akan kita gunakan dalam kombinasi untuk mencapai estimasi ketidakpastian yang lebih lengkap dan akurat.

Perbedaan antara kedua tipe ini terletak pada pendekatan yang kita gunakan dan sumber informasi yang kita andalkan. Tipe A lebih mengandalkan data pengukuran yang tersedia secara langsung, sementara tipe B mengandalkan penilaian subjektif atau pemodelan.

Dalam praktiknya, pendekatan tipe A dan tipe B sering kita gunakan dalam proses yang umum kita kenali sebagai “analisis ketidakpastian pengukuran”. Analisis ini melibatkan langkah-langkah seperti identifikasi faktor-faktor ketidakpastian, pengumpulan data pengukuran, analisis statistik, dan penilaian subjektif atau pemodelan.

Dalam kesimpulannya, pemahaman tentang tipe A dan tipe B dalam estimasi ketidakpastian pengukuran sangat penting dalam menilai keandalan dan keakuratan hasil pengukuran. Kombinasi antara pendekatan berbasis statistik dan penilaian subjektif atau pemodelan dapat membantu menghasilkan estimasi ketidakpastian yang lebih komprehensif.

Dengan demikian, praktisi pengukuran dapat membuat keputusan yang lebih terinformasi dan memahami tingkat ketidakpastian yang terkait dengan hasil pengukuran yang diperoleh.